Geometric Cipher (Original Algorithm)

Project Overview

The Geometric Cipher is a novel encryption algorithm that arranges text characters on regular polygons (triangles, squares, pentagons, etc.) in a spiral pattern. The cipher combines geometric positioning with optional character substitution, creating a two-layer encryption system. Characters are placed on concentric polygons and then read in a specific order to produce the ciphertext.

The final ciphertext is generated by reading the positioned characters from top to bottom, left to right - as if reading the geometric arrangement as normal text.

Core Concept

The cipher works by:

1. Splitting plaintext into blocks of size shape (number of polygon sides)
2. Positioning each block’s characters on a regular polygon
3. Applying rotation and direction transformations
4. Optionally applying a character substitution cipher
5. Reading the arranged characters in geometric order to produce ciphertext

Example: Basic Cipher

geometric_cipher("Ciphertext", shape=5, starting_pos=0, clockwise=True, turn_left=True)
# Output: 'tCireepthx'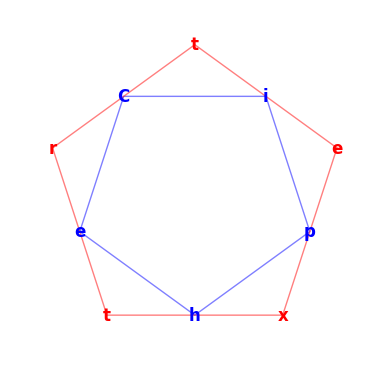

The input “Ciphertext” is arranged on a pentagon, with characters positioned at vertices. Reading from top to bottom produces the encrypted result.

Example: With Character Substitution

geometric_cipher("Ciphertext", shape=5, starting_pos=0, clockwise=True, turn_left=True, cipher=caesar_cipher)
# Output: 'uCisfepuhy'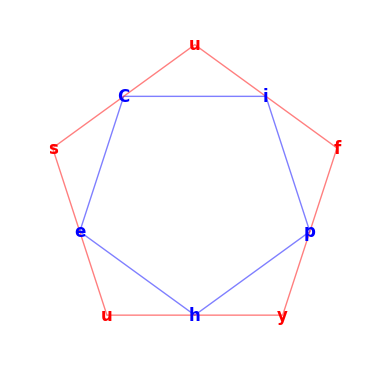

Adding caesar shifts each character by its layer number (the innermost is 0) before geometric positioning, creating a double-encrypted result that is extremely hard to break without knowing the shape.

Algorithm Details

Text Processing Pipeline

The process_text function handles the core transformation:

1. Character Substitution: Apply optional cipher to the block
2. Padding: Extend block to shape length if needed
3. Direction Reversal: Reverse text if clockwise=False
4. Rotation: Rotate the block based on starting_pos, block index, and turn_left parameter
5. Pairing: Split characters into pairs for symmetric polygon placement
6. Positioning: Calculate geometric coordinates using trigonometric functions

Coordinate Calculation

Characters are positioned using polar coordinates converted to Cartesian:

angle = π/2 + π * ((n + 1) % 2 + i * 2) / shape
radius = cos(π/shape)^(-n)
y = radius * sin(angle)
x = ±√(radius² - y²)

• n: Block index (determines polygon size)
• shape: Number of polygon sides
• i: Pair index within the block

The radius grows exponentially with each block, creating concentric polygons.

Character Ordering

The cipher sorts positioned characters by their y-coordinate (descending), then reads left to right for each y-level. This creates the final ciphertext by reading the geometric arrangement as if it were normal text.

Configuration Parameters

Parameter	Type	Default	Description
shape	int	4	Number of polygon sides (3=triangle, 4=square, 5=pentagon, etc.)
starting_pos	int	0	Initial rotation offset (0 to shape-1)
clockwise	bool	True	Direction of character placement
turn_left	bool	True	Rotation direction for subsequent blocks
cipher	function	identity	Optional character substitution function

Character Substitution Functions

Caesar Cipher Variant (caesar_cipher)

def caesar_cipher(txt, i):
    def shift_ascii(c):
        if 'A' <= c <= 'Z':
            return chr((ord(c) - ord('A') + i) % 26 + ord('A'))
        elif 'a' <= c <= 'z':
            return chr((ord(c) - ord('a') + i) % 26 + ord('a'))
        elif c.isdigit():
            return str((int(c) + i) % 10)
        return c

    return [shift_ascii(c) for c in txt]

Shifts depend on block index i, creating variable encryption strength across blocks. Supports:

• Uppercase letters (A-Z)
• Lowercase letters (a-z)
• Digits (0-9)

Decryption (caesar_decipher)

def caesar_decipher(txt, i):
    def shift_ascii(c):
        if 'A' <= c <= 'Z':
            return chr((ord(c) - ord('A') - i) % 26 + ord('A'))
        elif 'a' <= c <= 'z':
            return chr((ord(c) - ord('a') - i) % 26 + ord('a'))
        elif c.isdigit():
            return str((int(c) - i) % 10)
        return c

    return [shift_ascii(c) for c in txt]

Decryption Process

The geometric_decipher function reverses the encryption:

1. Order Reconstruction: Create dummy indices to track character positions
2. Geometric Positioning: Apply same transformations as encryption
3. Index Mapping: Determine original position of each ciphertext character
4. Reordering: Place characters back in original sequence
5. Character Reversal: Apply decipher function to reverse substitution

Returns a tuple: (reordered_text, text_blocks, final_plaintext)

Example: Decryption

geometric_decipher("tCireepthx", shape=5, starting_pos=0, clockwise=True, turn_left=True)
# Output: ('Ciphertext', [['C', 'i', 'p', 'h', 'e'], ['r', 't', 'e', 'x', 't']], 'Ciphertext')

geometric_decipher("uCisfepuhy", shape=5, starting_pos=0, clockwise=True, turn_left=True, decipher=caesar_decipher)
# Output: ('Ciphesufyu', [['C', 'i', 'p', 'h', 'e'], ['s', 'u', 'f', 'y', 'u']], 'Ciphertext')

Visualization

The visualize_geometric_cipher function generates matplotlib plots showing:

• Character positions on polygon vertices
• Concentric polygons for multiple blocks (color-coded by depth)
• Geometric arrangement before reading

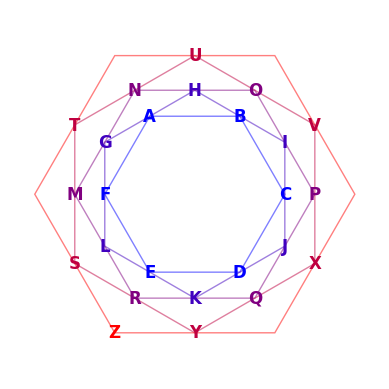
Color Encoding:

• Blue (inner): First block (n=0)
• Gradient to red: Subsequent blocks
• Polygon transparency: 50% for edge visibility

Security Analysis

Strengths:

• Unconventional character ordering resistant to frequency analysis
• Variable encryption with block-dependent transformations
• Customizable parameters increase keyspace
• Optional layered encryption (geometric + substitution)

Weaknesses:

• Deterministic algorithm vulnerable to known-plaintext attacks
• Geometric positioning patterns may be recognizable with multiple samples

Use Cases

• Educational cryptography demonstrations
• Artistic text encoding
• Low-security obfuscation for puzzles/games
• Steganographic applications (embed in geometric art)

Example Applications

Short Message

geometric_cipher("Hello", shape=5, starting_pos=2, clockwise=False, turn_left=False)
# Output: 'lloeH'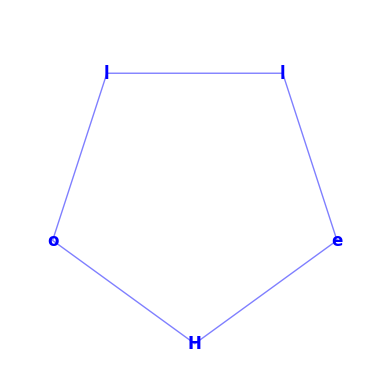

Long Text

geometric_cipher("The quick brown fox jumps over the lazy dog", shape=6, starting_pos=1, clockwise=True, turn_left=True, cipher=caesar_cipher)
# Output: 'j uzxinpl jqhempd  syT hvgjc suqm qsq aweyf'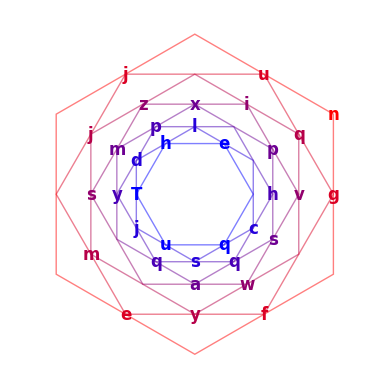

Custom Shape

geometric_cipher("Octagon", shape=8, starting_pos=0, clockwise=True, turn_left=True)
# Output: 'Octnaog'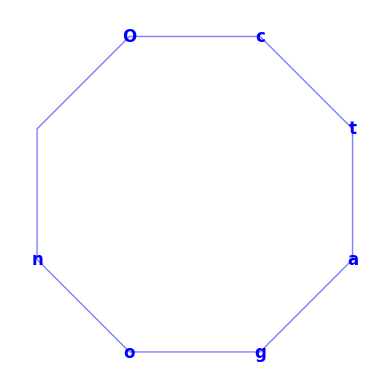

Implementation Notes

• Uses Python’s math library for trigonometric calculations
• Matplotlib required for visualization (matplotlib.pyplot, matplotlib.patches)
• Floating-point rounding to 10 decimal places prevents coordinate drift
• Handles odd-length blocks by placing center character at polygon center

Conclusion

The Geometric Cipher demonstrates how spatial transformations can create encryption beyond traditional character substitution. While not cryptographically secure for sensitive data, it provides an intuitive visualization of how geometric mathematics can encode information. The customizable parameters and optional substitution layer make it a flexible tool for educational purposes and creative text obfuscation.